Book Review: History of Mathemathics


History of Mathematics, 1941
(Histoire des Mathématiques, 1941)
Marcel Bol
Marcel Boll’s book “History of Mathematics” was written to speak to large masses about the development of mathematical thought and critically evaluate historical approaches towards mathematics. Originally written in French, he explores the evolution of mathematics from ancient civilizations like Babylon, Egypt, Greece, through the Middle Ages into the modern times. Boll approaches the field of mathematics as an experimental science which is invented by the human mind, is open to evolution and is falsifiable. He presumes that mathematics is an abstract science which has a broad area of application. Throughout the book, his critical voice is so strong and sometimes sharp while judging the current mathematics education of his time and criticizing the followers of old Greek philosophers and mathematicians.
In the History of Mathematics, Marcel Boll doesn’t try to give a historical chronology or include the contribution of every mathematician. It seems that he aims to bring the reader a sense of understanding how some basic concepts and mathematical activities such as counting, operations or sets of numbers evolved and to which need they responded in the history. In the first two chapters, he traces the appearance of four operations and the spread of numbers from counting numbers to negative numbers. Before discussing the idea of infinity, he introduces the emergence of algebraic expressions and gives a critique about how the ancient Greek understanding slowed down the development of modern mathematics. In those times, algebraic symbolization was lacking and for Boll, they were kind of against the power of algebra, and abstract mathematical thought, instead they were passionate about the forms of objects. For the western world, there was a long dark gap until Descartes came into the scene and the foundation of algebra started. Boll mentions two important names before the time of Descartes in the progress of algebra, Archimedes and Vieta, which the prior was thinking beyond his time and introduced “infinitesimals” and the latter took important step for modern algebra by using variables as parameters in the equations.
One of the interesting critiques of the writer appears on the problem of “Squaring a Circle”. He believes that ancient Greek mathematicians didn’t think about the “numerical space”. This term might evolve due to an interpretation based on the translation; however, what he tries to say is that the Greek mathematicians departed by the experimental features of mathematics and our minds, which lead to preventing us from imagining space through numbers until Descartes. The problem of squaring circle is a consequence of this fact. It was a greatly exaggerated problem for Boll as they tried to solve it only by using a compass and ruler. He believes that “for real mathematicians” to find approximate approaches to solve the problem of drawing squares having the same area as the circle given by the primitive methods was a laughing stock. This case didn’t change until 1882 when the number is accepted as a transcendental number and it was understood that it is impossible to give a perfect drawing (p.80, Boll).
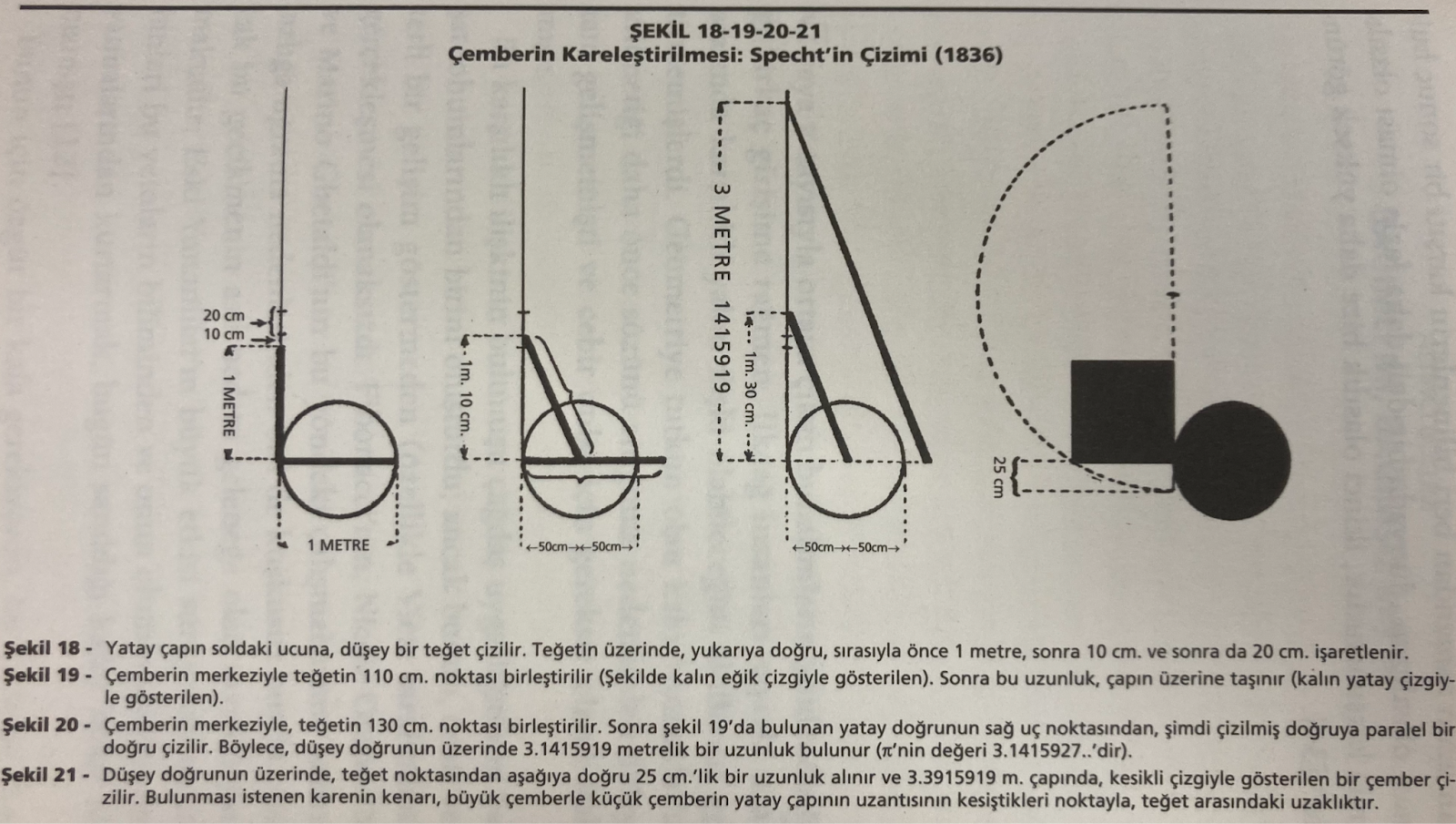
Boll’s critiques on the traditional approaches toward mathematics could be understood from a progressivist viewpoint; but I think that they should be evaluated in their own context and time. Considering an effort of using simple tools for a geometric solution as a “trip for biscuits” might be unfair in the conditions of the mathematicians and maybe against the nature of human thought. I believe that it is more illuminating to focus on what was the use of traditional approaches and modern approaches from an objective perspective to understand benefits. I agree with the writer’s critics on highly focusing on Euclidean geometry by not teaching other geometries much in secondary education (he talks about the 1940s) and suggesting Mathematics teachers to consider teaching correct reasoning by widening the students’ perspectives.